VECTORES

Es un ente matemático como la recta o el plano. Un vector se representa mediante un segmento de recta, orientado dentro del espacio euclidiano tridimensional. El vector tiene 3 elementos: módulo, dirección y sentido.​ Los vectores nos permiten representar magnitudes físicas vectoriales, como las mencionadas líneas abajo.

En matemáticas se define vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta ${\displaystyle \mathbb {R} }$, en el plano ${\displaystyle \mathbb {R} ^{2}}$ (bidimensional), o en el espacio ${\displaystyle \mathbb {R} ^{3}}$ (tridimensional).

SUMA Y RESTA DE VECTORES

La  suma y resta de dos vectores A  y B, da como resultado otro vector, es decir, A + B = C   y   A – B = C

Para la suma y resta de vectores se aplican distintos métodos dependiendo si los éstos tienen o no la misma
dirección. Los principales métodos son: el método directo, el del triángulo y el paralelogramo.

SUMA DE VECTORES

Para sumar dos vectores A  y B se suma A  con el vector B, es decir, se suman las componentes de cada vector:

A + B = (Ax + Bx, Ay + By, Az + Bz)

Ejemplo: Sean A = (3, 2, -4) y B = (-3, 2, 7), calcula el vector A + B.

A + B = ( 3 + (-3), 2 + 2, -4 – 7) = (0, 4, 3)

SUMA DE DOS VECTORES CON LA MISMA DIRECCIÓN Y EL MISMO SENTIDO

1. Dibujamos el vector B a continuación del vector A, de manera que sean consecutivos, respetando sus módulos, direcciones y sentidos.
2. El vector suma A + B tiene como módulo la suma de los módulos de ambos, la misma dirección y el mismo sentido de los vectores dados.

El vector resultante A + B tiene como módulo la suma de A  y de B, la misma dirección y el mismo sentido que A  y B.

El vector resultante A + B tiene como módulo la suma de A  y de B, la misma dirección y el mismo sentido que A  y B.

SUMA DE DOS VECTORES CON LA MISMA DIRECCIÓN Y EL SENTIDO 

OPUESTO

1. Dibujamos el vector B a continuación del vector A, de manera que sea consecutivos, respetando sus módulos, direcciones y sentidos.
2. El vector suma tiene como módulo la diferencia de los módulos de ambos, la misma dirección y el sentido del vector mayor.

El vector resultante A + B tiene como módulo la diferencia de A  y de B, la misma dirección y el mismo sentido
 que A  y B.

 SUMA DE DOS VECTORES CON DISTINTA DIRECCIÓN

Para sumar dos vectores A  y B que forman un ángulo entre sí, se usan dos métodos: el método del triángulo y el
método del paralelogramo.

MÉTODO DEL TRIANGULO

1. Dibujamos los vectores de forma consecutiva, es decir, el origen de B tiene que coincidir con el extremo A.
2. El vector suma A + B tiene como origen, el origen de A  y como extremo, el de B.

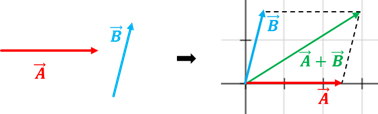
LEY O MÉTODO DE PARALELOGRAMO

1. Dibujamos el vector A en el origen de un plano cartesiano respetando su módulo, dirección y sentido.
2. Dibujamos en el origen de A, el vector B respetando su módulo, dirección y sentido.
3. Se trazan rectas paralelas a cada vector formando un paralelogramo.
4. El vector resultante será la diagonal del paralelogramo que inicia en el origen del plano cartesiano.
5. 

RESTA DE VECTORES

Para restar dos vectores A y B se suma A con el opuesto de vector B, es decir:

A – B = A + (- B)

Las componentes del vector A – B se obtienen restando sus componentes.

A – B = (Ax – Bx, Ay – By, Az – Bz)

Ejemplo: Sea A = (5, 2, 4) y B = (-3, 5, 9), calcula el vector A – B.

A – B = ( 5-(-3), 2-5, 4-9) = (8,-3,-5)

MÉTODO DEL VECTOR OPUESTO

Para restar dos vectores A y B:

1. Como el vector B es el sustraendo debemos dibujar su vector opuesto; por ello dibujamos un vector igual a B pero de sentido opuesto.
2. Aplicamos la ley del paralelogramo.

MÉTODO DEL TRIANGULO

1. Dibujamos en el origen de A, el vector B respetando su módulo, dirección y sentido.
2. El vector resultante A – B tendrá como origen el extremo de B (vector sustraendo)  y 

     como extremo, el extremo de A  (vector minuendo).